Предлагаю вниманию коллег приемы обучения и виды заданий, которые максимально гармонично могут интегрироваться в учебное занятие, не требуя больших временных затрат и при этом внося вклад в формирование функциональной грамотности учащихся.

С 2023/2024 года с целью получения информации о сформированности функциональной грамотности учащихся 10 класса (1 курса) в Беларуси проводится национальное исследование качества образования (НИКО). Функциональная грамотность — это выработанная в процессе учебной и практической деятельности интегративная готовность к нахождению оптимальных способов решения жизненных задач и созданию нового в различных сферах (человек, социум, природа, материальная и духовная культура). Формирование функциональной грамотности учащихся — одна из основных задач современного образования. На сегодняшний день конечной целью обучения является практическое применение полученных знаний в различных жизненных ситуациях, а не накопление абстрактной информации.
Для определения стратегии обучения математике целесообразно изучить тренировочные задания, предлагаемые при проведении исследования НИКО, размещенные в открытом доступе сети интернет, и материалы, рекомендуемые для подготовки к республиканской контрольной работе. Также могут быть использованы сборники эталонных заданий контролирующего и тренировочного характера, предложенные российскими коллегами, в тех случаях, когда они согласуются с нашими учебными программами. Задания там достаточно громоздкие, лишь точечно касаются определенного программного материала и поэтому с небольшой вероятностью будут использованы на учебных занятиях по математике. Но на уроке прежде всего должен быть изучен материал по программе, на который отведено количество часов, необходимое для его усвоения учащимися. Поэтому посвятить целое занятие решению одной масштабной задачи, максимально ориентированной на формирование функциональной грамотности учащихся, можно, только если образовался резерв времени или в учреждении образования проводится факультатив на основе утвержденной программы.
Среди заданий ЦТ и ЦЭ прошлых лет встречаются задания, ориентированные на проверку способности применять полученные знания в различных жизненных ситуациях. Такие задания целесообразно использовать на уроках, посвященных изучению соответствующего материала.
С целью внесения вклада в формирование финансовой грамотности учащихся при подготовке к учебным занятиям имеет смысл воспользоваться заданиями республиканских олимпиад, размещенными на едином портале финансовой грамотности.
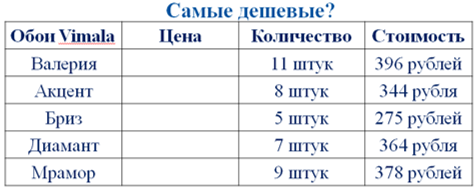
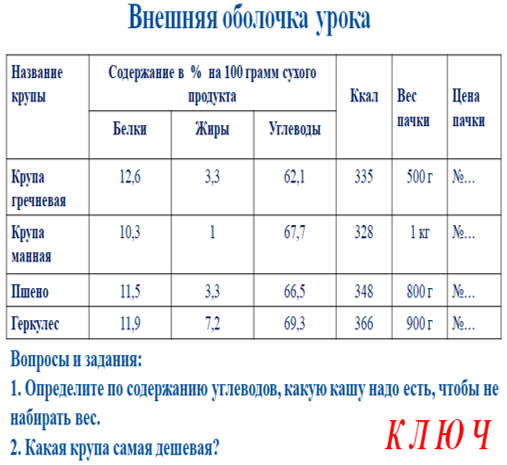
В качестве приемов, направленных на формирование элементов финансовой грамотности, могут использоваться как устный счет с определенной фабулой, так и внешняя оболочка урока, в ключе
к которой в соответствие ответам к заданиям ставятся актуальные данные для заполнения таблицы.
Значительным потенциалом с позиции формирования элементов функциональной грамотности обладает задачный материал, в большей степени практико-ориентированные и компетентностно ориентированные задачи, которые учителю чаще всего необходимо найти или составить самостоятельно. В действующих учебных пособиях преобладают либо абстрактные (“Найти периметр прямоугольника, если его длина равна 3 м, ширина 4 м”), либо контекстные задачи (“Найти длину бордюрной ленты, ограничивающей прямоугольную клумбу размером 3 на 4 м”). Практико-ориентированную задачу отличает связь с конкретными фактами из жизни (“Интернет-магазин Deal предлагает деревянную баню-бочку размером 3 на 4 м. Сколько погонных метров бордюра надо приобрести, чтобы ограничить площадку для такой бани?”), а в компетентностно ориентированной задаче еще и делается акцент на личной заинтересованности того, кто выполняет задание (“Вы решили приобрести в интернет-магазине Deal деревянную баню-бочку размером 3 на 4 м. Сколько вы заплатите фирме “Строймолл” за бордюр, чтобы ограничить площадку для вашей бани, если погонный метр такого бордюра предлагается по цене 5 рублей?”). При этом в современных учебных пособиях по геометрии имеются задания, претендующие на право называться практико-ориентированными. Они размещены в рубриках “Реальная геометрия” или “Моделирование”.
Несмотря на то, что решение практико-ориентированных и компетентностно ориентированных задач в большой степени способствует формированию функциональной грамотности учащихся, не на каждом уроке уместно их использование.
Отдельного внимания заслуживают задания, предполагающие применение рационального способа решения. Они также способствуют формированию и критического мышления, и приемов мыслительной деятельности, и креативного мышления, и в целом функциональной грамотности.
Пример 1. Решите рациональным способом уравнение 13х2 – 20х + 7 = 0.
Для решения этого квадратного уравнения можно воспользоваться и стандартным дискриминантом, и дискриминантом, уменьшенным в 4 раза (коэффициент при х четный), и приемом “переброса” в сочетании с теоремой, обратной теореме Виета. Но самым рациональным способом, конечно же, является использование того факта, что сумма коэффициентов равна нулю, а значит, первым корнем является число 1, а вторым с/a = 7/13. Такие уравнения, как и уравнения, в которых сумма крайних коэффициентов равна среднему коэффициенту (тогда первый корень уравнения равен –1, а второй –с/a), целесообразно как можно чаще использовать в качестве устных упражнений на этапе актуализации опорных знаний.
Пример 2. Решите рациональным способом задачу: “Найдите площадь треугольника, длины сторон которого равны 21, 28, 35”.
Для решения этой задачи можно воспользоваться и формулой Герона, и теоремой, обратной теореме Пифагора в стандартном виде. Но наиболее оптимальный вариант — обратить внимание на то, что предложен египетский треугольник с коэффициентом 7. Имеет смысл регулярно приносить на занятия по геометрии задания, в которых идет речь о египетском треугольнике с коэффициентом или о Пифагоровой тройке, также увеличенной в какое-либо число раз.
В отдельный блок можно выделить задания, которые имеют нетиповой формат и при этом также обладают немалым потенциалом с позиции формирования функциональной грамотности учащихся. Это задания с нестереотипной формулировкой; задания, в которых содержится лишняя, но не противоречивая информация; невыполнимые задания, в которых заключена противоречивая информация; задания, имеющие несколько решений; задания с недостающими данными и решенные задания, в решении которых содержится ошибка, которую надо найти. Остановлюсь подробнее на каждом типе заданий.
Пример 3. Задание, в котором содержится лишняя, но не противоречивая информация. В равнобедренной трапеции АВСD (ВС || АD) диагонали взаимно перпендикулярны. Найдите площадь четырехугольника, вершины которого являются серединами сторон трапеции, если АВ = 4,
АС = 6.
Четырехугольник, площадь которого требуется найти, является квадратом со стороной, равной половине диагонали трапеции. Длина боковой стороны трапеции оказалась не востребована.
Такого типа задания развивают способность критически оценивать предложенную информацию, абстрагироваться от лишних данных, вносят вклад в формирование приемов мыслительной деятельности.
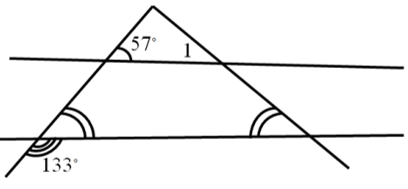
Пример 4. Задание с нестереотипной формулировкой. Найдите по рисунку величину угла 1.
Не трудно найти величину угла 2 как смежного с углом, равным 133°.
Тогда Ð3 = Ð2 = 180° – 133° = 47°. Дальше учащиеся могут ошибочно предположить, что Ð1 = Ð3 как соответственные, но прямые не параллельны и свойство не работает. Используя свойство суммы углов треугольника дважды, находим, что Ð1 = 37°.
Такие задания учат критически воспринимать предложенные факты и мыслить нешаблонно.
Пример 5. Задание с несколькими решениями. В трапеции АВСD (ВС || АD) точка пересечения диагоналей делит АС в отношении 2 : 3. Найдите площадь трапеции, если площадь треугольника АВС равна 6.
Задание помогает бороться с шаблонным мышлением. Учащиеся стереотипно считают, что основание ВС у трапеции всегда меньше основания АD, поскольку именно такой вариант чаще всего предлагается в учебных пособиях и дидактических материалах. Здесь же возможны два варианта. Тогда получаем 15, если ВС < AD, или 10, если ВС > AD.
Рассуждения при решении таких задач помогают формировать способность видеть различные выходы из сложившихся ситуаций, мыслить многовекторно.
Пример 6. Задание, содержащее противоречивую информацию (невыполнимое).
В равнобедренном треугольнике один из внешних углов равен 50°, а два угла треугольника, не смежных с ним, относятся как 2 : 3. Найдите угол при основании.
Поскольку данный внешний угол острый, то он при вершине, а два угла треугольника, не смежные с данным, — при основании, а значит, равны и не могут относиться как 2 : 3.
Такого типа задания учат распознавать фейковую информацию, формируют критическое мышление и вносят вклад в формирование приемов мыслительной деятельности.
Пример 7. Задание с недостающими данными. В параллелограмме АВСD биссектриса угла А пересекает сторону СD в точке К. Найдите периметр параллелограмма, если ВС = 2. Что можно добавить в условие задачи, чтобы ее можно было решить?
Добавить можно, например, СК : КD =
1 : 2. Тогда Р = 10.
Такие задания формируют критическое мышление и требуют применения приемов мыслительной деятельности.

Особую ценность для учащихся имеют задания, содержащие в решениях ошибки, которые необходимо найти. Далеко не многие учащиеся способны находить собственные ошибки при проверке выполненных заданий. Такую способность, безусловно, необходимо тренировать. При этом опять-таки вносится вклад в развитие умения распознавать фейковую информацию и критически воспринимать факты.
Все перечисленные выше задания способствуют формированию как математической грамотности в частности, так и функциональной грамотности учащихся в целом. Такие задания целесообразно включать в этап актуализации опорных знаний при изучении подходящих тем. Они в большинстве своем не предназначены для осуществления контроля знаний, поэтому, как правило, не имеют аналогов в дидактических материалах. Они выполняют другую функцию — прежде всего вносить вклад в формирование функциональной грамотности учащихся, хотя и качество знаний при этом, безусловно, повышается.
Принимая во внимание значимость таких заданий, на одном из заседаний республиканской творческой группы учителей математики решили создать сборник “Математика с подвохом”. Первые наработки были презентованы на республиканских вебинарах для учителей математики. В журнале “Математика и физика” в рубрике “У дапамогу педагогу” в качестве анонса было опубликовано две статьи. Не каждый учитель будет регулярно разрабатывать подобные задания к учебным занятиям, а вот воспользоваться готовыми материалами могут многие.
В завершение необходимо отметить, что, с одной стороны, очень многие задания, направленные на формирование математической и финансовой грамотности, связаны с понятиями “экономия” и “выгода”, но, с другой стороны, эти понятия иногда вызывают спорные вопросы и требуют включения критического мышления и здравого смысла. Выбирая товар, используя различные предложения в интернет-магазинах, не всегда стоит ориентироваться на самую низкую цену. Покупая овощи на рынке из двух предложений “ящик весом 10 кг за 22 рубля” и “1 кг за 2,75 рубля”, надо подумать, будет ли выгоднее купить помидоры по более низкой цене за килограмм. Продать велосипед по объявлению по более высокой цене, чем продать его заинтересованному в покупке другу — вопрос, касающийся в большей степени норм морали и качеств личности, чем выгоды и экономии. Поэтому, стремясь внести вклад в формирование функциональной грамотности, всегда надо руководствоваться здравым смыслом и приоритет отдавать воспитанию лучших личностных качеств.
Елена ПРОТАСЕВИЧ,
учитель математики квалификационной категории “учитель-методист”
средней школы № 1 Дрогичина, член клуба “Хрустальный журавль”




















