Паспяховасць чалавека сёння вызначаецца тым, наколькі хутка ён умее ўсебакова аналізаваць сітуацыю, прапаноўваць нестандартныя спосабы вырашэння праблем. У сувязі з гэтым асаблівую актуальнасць набывае праблема навучання малодшых школьнікаў рашэнню нестандартных задач.

Нестандартныя задачы заўсёды падаюцца ў займальнай форме, яны праганяюць інтэлектуальную ляноту, выпрацоўваюць звычку да разумовай працы, выхоўваюць настойлівасць у пераадоленні цяжкасцей.
Пытанні, якія патрабуюць разгляду чагосьці з нязвыклага боку, нярэдка ставяць дзяцей у тупік. І гэта зразумела, бо іх гэтаму не вучылі. Убачыць нешта па-новаму, не так, як усе, і не так, як ты бачыў раней, — вельмі няпростая задача. Але гэтаму можна навучыць, калі накіраваць працэс навучання на развіццё творчых здольнасцей навучэнцаў сістэмай задач, пры рашэнні якіх у дзяцей праяўляецца не толькі цікавасць да ведаў, але і да самога працэсу пошуку.
Прымяненню ў пачатковай школе нестандартных матэматычных задач папярэднічае вялікая падрыхтоўчая работа па іх адборы. Задачы павінны валодаць наступнымі асаблівасцямі: быць актуальнымі з пункту гледжання вучняў; абуджаць у іх цікавасць і жаданне знайсці рашэнне; патрабаваць для свайго рашэння ад навучэнцаў уяўлення і творчых здольнасцей; быць адначасова дастаткова складанымі і даступнымі для вучняў; падахвочваць дзяцей да пошуку новых прынцыпаў, фактаў і метадаў рашэння (вынікам якога з’яўляецца набыццё новых ведаў); дапускаць розныя спосабы рашэння і варыятыўнасць вынікаў рашэння (ці нават адсутнасць такога); утрымліваць у асобных выпадках дадзеныя і факты, лішнія для ажыццяўлення рашэння (або мець іх у недастатковай для рашэння колькасці); дапускаць хуткае рашэнне і рашэнне на працягу доўгага часу работы; патрабаваць умення прымяняць аналіз і сінтэз у якасці метадаў іх рашэння.
Вось некалькі метадаў рашэння, якія я выкарыстоўваю.
1. Арыфметычны — вынік рашэння задачы знаходзіцца шляхам выканання арыфметычных дзеянняў.
Для паліву 8 яблынь і 4 груш хлопчыкі прынеслі 140 вядзёр вады. Колькі вядзёр вады вылілі пад яблыні і колькі пад грушы, калі на паліў адной яблыні патрэбна вады ў 3 разы больш, чым на паліў адной грушы?
Калі за зыходнае разгледзець адносіны паміж колькасцю дрэў (8 яблынь, 4 грушы), то адказ на пытанне задачы можа быць атрыманы шляхам выканання наступных дзеянняў.
1) 8 : 4 = 2 (раз.) — яблынь больш, чым груш;
2) 2 · 3 = 6 (раз.) — вады вылілі больш пад яблыні;
3) 1 + 6 = 7 (част.) — у агульным аб’ёме вады;
4) 140 : 7 = 20 (вядз.) — выкарысталі на паліў усіх груш;
5) 140 – 20 = 120 (вядз.) — выкарысталі на паліў усіх яблынь.
2. Алгебраічны — адказ знаходзіцца шляхам складання і рашэння ўраўнення.
Вышэй прапанаваную задачу рашым алгебраічным метадам. Пазначым праз x колькасць вядзёр вады, вылітых пад адну грушу, тады на паліў адной яблыні трэба 3x вядзёр вады. Паколькі палілі 4 грушы, 8 яблынь і выкарысталі 140 вядзёр вады, складзём ураўненне: 4x + 8 · 3x = 140. Рашыўшы яго, атрымліваем x = 5. Значыць, для паліву ўсіх груш спатрэбілася 5 · 4 = 20 вядзёр вады, а яблынь — 140 – 20 = 120.
Праверку можна выканаць, суаднёсшы знойдзены вынік з умовай задачы або рашыўшы задачу іншым спосабам або метадам.
3. Графічны — дазваляе знайсці адказ без выканання арыфметычных дзеянняў, абапіраючыся толькі на чарцёж.
З двух пунктаў насустрач адзін аднаму выехалі два веласіпедысты. Першы праехаў 1/3 шляху, другі — 4/8 шляху. Ці адбылася сустрэча веласіпедыстаў?
Пакажам адлегласць паміж пунктамі адрэзкам, колькаснае значэнне даўжыні якога дзеліцца адначасова на 3 і на 8 — для канкрэтнай задачы зручней пабудаваць адрэзак даўжынёй 24 адзінкавыя адрэзкі.

Абапіраючыся на чарцёж, можна сфармуляваць адказ: “Сустрэча не адбылася”.
4. Практычны — адказ знаходзіцца з дапамогай непасрэдных дзеянняў з прадметамі (малюнак, схема, табліца).
На стаянцы ля Мішынага дома было 8 транспартных сродкаў: двухколавыя матацыклы і легкавыя аўтамабілі. Міша налічыў у іх 22 колы. Колькі матацыклаў і колькі аўтамабіляў было на стаянцы?
Пералікам установім, што калі ў кожнага транспартнага сродку было б толькі 2 колы, то ўсяго ў іх было б 16 колаў (2 · 8 = 16). Зробім сімвалічны малюнак або выкладзем адпаведную колькасць, напрыклад, колаў.
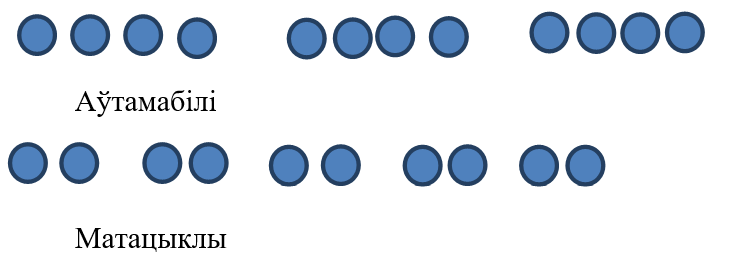
Але па ўмове задачы вядома, што ўсяго было не 16, а 22 колы. Такім чынам, трэба дадаць яшчэ 6 колаў (22 – 16 = 6).
Да трох першых транспартных сродкаў дададзім па 2 колы, бо ў кожнага аўтамабіля — 4 колы.
5. Метад здагадкі, або метад адной фальшывай здагадкі. Сутнасць яго ў наступным. Вылучаецца гіпотэза: няхай адказ задачы будзе такім. Шляхам разваг і вылічэнняў правяраецца прынятая гіпотэза, гэта значыць, устанаўліваецца, ці выконваюцца пры ёй умовы задачы. У выпадку, калі лік не адпавядае ўмовам задачы, знаходзяць адхіленне гіпотэзы ад дакладнага адказу: калі адхіленне адмоўнае, гэта значыць, гіпотэза меншая за адказ, то адхіленне дадаецца да гіпотэзы; калі гіпотэза большая за адказ, гэта значыць, адхіленне станоўчае, то яно аднімаецца ад гіпотэзы; калі адхілення няма, то гіпотэза прымаецца за адказ задачы.
6. Метад перабору — заключаецца ў пераборы магчымых варыянтаў.
Трэба пасадзіць 22 турыстаў у двухмесныя і чатырохмесныя лодкі. Колькі тых і іншых лодак спатрэбіцца, калі ўсяго лодак 8?
Аформім паслядоўны перабор усіх варыянтаў у табліцу.
|
Двухмесныя лодкі |
Чатырохмесныя лодкі |
Усяго турыстаў |
|
1 |
7 |
30 > 22 |
|
2 |
6 |
28 > 22 |
|
3 |
5 |
26 >22 |
|
4 |
4 |
24 > 22 |
|
5 |
3 |
22 = 22 |
Пры ўключэнні нестандартных задач навучанне ажыццяўляецца дзейсным метадам, калі дзеці не атрымліваюць веды ў гатовым выглядзе, а адкрываюць іх у працэсе самастойнай даследчай дзейнасці. Я прапаную навучэнцам сістэму пытанняў і заданняў, якія падводзяць іх да самастойнага адкрыцця новай уласцівасці або адносін.
Нестандартныя задачы фарміруюць у школьнікаў высокую матэматычную актыўнасць, якасці, уласцівыя творчай асобе: гнуткасць, арыгінальнасць, глыбіню, мэтанакіраванасць, крытычнасць мыслення.
Ала ШАМІНСКАЯ,
настаўніца пачатковых класаў
Лудчыцкай сярэдняй школы Быхаўскага раёна Магілёўскай вобласці




















