Контекстные задания по математике призваны помочь учащимся понять важность изучения математики и ее применения в повседневной жизни.

Задачи такого вида направлены на развитие математической, читательской и естественнонаучной грамотности. Например, задание может быть связано с расчетом бюджета для покупки продуктов в семье на неделю или с планированием маршрута путешествия. Еще одним преимуществом таких заданий является их интерактивный характер. Учащимся предлагается активно участвовать в процессе решения, а не просто механически выполнять упражнения. Вместо того, чтобы решать задачу на бумаге, можно предложить разобрать реальные ситуации, в которых они должны использовать математические знания.
Хочу привести несколько примеров из собственной практики.
8 класс. Тема “Подобные треугольники”
Задача 1. В конструкторское бюро яхт-клуба за помощью обратились два друга. Некоторое время назад они приобрели две абсолютно одинаковые яхты, но во время путешествия заметили, что одна из яхт идет быстрее по ветру. Выяснилось, что пошив парусов заказывали в разных ателье. Произведите необходимые измерения и расчеты, исследуйте параметры и особенности парусов обеих яхт. На основании полученной информации предположите причину, из-за которой скорость могла быть разной. Обратите внимание на расположение линий парусов (для учителя: на одном рисунке линии парусов изображены параллельно, на другом нет).
Задача 2. На кафедре математики университета раздался звонок. Трубку взял студент, который занимался научной работой. Звонил адвокат с историей о том, что недавно возле одного из торговых центров у женщины грабитель вырвал сумочку. На улице было темно, рассмотреть его лицо было невозможно, но видеокамера запечатлела размер тени грабителя. Студент ответил, что задача сводится к решению подобных треугольников и человек, которого обвиняют в воровстве, невиновен, так как его рост всего лишь 170 см. Прав ли был студент, если длина тени предполагаемого грабителя 164 см, а длина тени студента 150 см при росте 172 см? Вычислите рост грабителя.
9 класс. Тема “Формула длины отрезка с заданными координатами. Уравнение окружности”
Задача. По проекту администрации вокруг города N планировалась постройка кольцевой дороги на расстоянии 6 км от центра города. Местоположение города было задано координатами (4;3). В тот момент, когда началось строительство, внезапно поступил звонок, что на некоторых участках пути строительства находится несколько объектов, которые подлежат сносу. Возможно ли определить, не выезжая на место, все ли объекты необходимо сносить? Ваши предположения обоснуйте и аргументируйте. Координаты объектов А (2;7), В (4;9), С (3;5).
Тема “Вписанная и описанная окружности в треугольник”
Задача. а) В одно из конструкторских бюро поступил заказ рассчитать длину объездной кольцевой дороги для большегрузных машин вокруг города N, учитывая, что в городе три центральные улицы. Какие измерения необходимо сделать? Как рассчитать радиус кольцевой дороги?
б) В тот же день поступил заказ рассчитать радиус клумбы в парковой зоне, учитывая, что дорожки в парке пересекаются под углом 60⁰ и клумба должна находиться между всеми тремя дорожками одновременно.
Тема “Теорема синусов и косинусов”
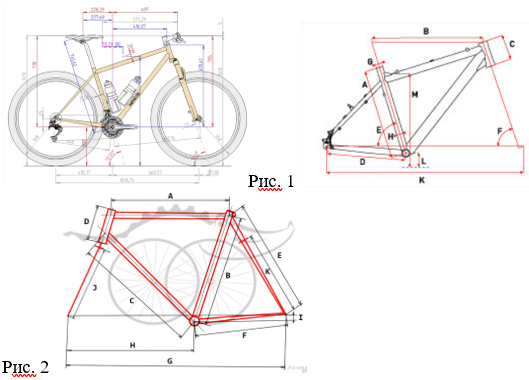
Задача. Выполните необходимые измерения и рассчитайте углы, крепления рам и вилки в велосипедах современного образца (рис. 1) и советского образца (рис. 2). Найдите сходство и отличие конструкций, определите, влияют ли данные параметры на скорость движения, на износостойкость машины.
11 класс. Тема “Объем прямоугольного параллелепипеда”
Задача. В строительную компанию обратился молодой человек: “Меня зовут Владимир, мне 27 лет. Живем мы с женой с родителями в многоэтажном доме в двухкомнатной квартире. У нас была мечта построить собственный дом, а не квартиру. Этап бумажной волокиты и проекта был благополучно нами пройден. Помогите рассчитать оптимальную сумму затрат для заливки фундамента, учитывая нюансы с закупкой материалов” (рис. 3).
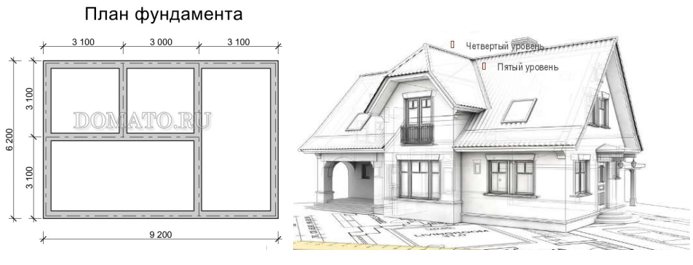
План работы специалиста компании:
1) перевести единицы измерения в метры; 2) определить внешнюю и внутреннюю площадь фундамента; 3) найти их разность, то есть вычислить площадь фундамента (ширина 0,3 м); 4) вычислить объем фундамента, если его ширина 0,3 м, глубина 0,5 м; 5) рассчитать количество мешков цемента для фундамента и его стоимость, если на 1 м3 бетоносмеси приблизительно необходимо 5,2 мешка весом 50 кг; стоимость 1 мешка 50 кг от 9 руб.; 25 кг от 5,18 руб., стоимость доставки 30 руб.
Тема “Цилиндр: площадь боковой поверхности, объем цилиндра”
Задача. К новогодним праздникам Аня решила подарить друзьям ароматические свечи. Приобрела модельный воск для свечей (стоимость за 1 кг — 23 руб.), аромамасло (5 руб.) и рулон бумаги 10 м для упаковки (11 руб.). Вычислите, какое количество свечей получится изготовить для подарков, если высота свечи 12 см, диаметр 5 см. Рассчитайте возможный остаток упаковочной бумаги, а также затраты, в том числе если использовать для упаковки крафтовые пакеты (40 шт. — 10 руб.), и возможную выгоду, если стоимость такой же аромасвечи в магазине 7 руб.
Тема “Конус”
Задача. а) В компанию “Розмарин”, занимающуюся кейтерингом, поступил срочный заказ. Необходимо рассчитать количество посыпки на торт “Муравейник”, если диаметр его основания 30 см, высота 2,5 дм и на каждый квадратный сантиметр торта посыпки требуется 1,2 г. Обратите внимание, что тортов заказано 5 штук.
б) Стоимость торта “Муравейник” диаметром 26 см и высотой 18 см составляет 15 руб. Ребята решили продать данный торт порционно, используя пластиковые стаканчики для определения одной порции. Проведите измерения и рассчитайте максимальную прибыль, которую возможно получить, а также сколько понадобится глазури для пирожных, если на 1 кв. см необходимо 0,8 г глазури.
Задача. Вы с друзьями решили реализовать бизнес-план по продаже мороженого. Закупили партию 300 кг мороженого в контейнерах и решили продавать его в рожках. Рассчитайте возможную прибыль с учетом затрат на покупку рожков (10 шт. — 5,7 руб.), упаковки (100 шт. — 8 руб.). Первоначальную стоимость при продаже мороженого 80 г решили установить 1,4 руб. Автомат-наполнитель можно отрегулировать только на заполнение рожков количеством определенного объема. Рассчитайте параметр объема, который необходимо задать автомату. Учтите количество затрат при покупке весового мороженого, если контейнер 1,3 кг стоит 16,27 руб.
Тема “Объем сферы”
Задача. а) Набор шоколадных бомбочек с маршмеллоу из 3 штук стоит 15 руб. Вычислите возможную прибыль при изготовлении таких наборов, если 100 г шоколада стоит 4 руб., цена 200 г маршмеллоу 6 руб. Для изготовления 1 бомбочки необходимо 10 г маршмеллоу. Вычислите объем и массу шоколада для бомбочки, если диаметр ее внешней и внутренней поверхности 5 см и 48 мм соответственно. Для вычисления массы дополнительно воспользуйтесь данными плотности шоколада из интернета. Рассчитайте возможное количество получившихся бомбочек для 1500 кг шоколада.
б) Произведите измерения и вычислите объем мякоти и кожуры апельсина (грейпфрута), форма которого максимально приближена к форме сферы. Сколько штук фруктов необходимо для получения 1 литра сока с мякотью, если отходы с очищенного фрукта составляют 20%?
Такие задачи пригодятся в методической копилке любого учителя и позволят разнообразить учебное занятие. Возможно, когда-нибудь именно такая задача подтолкнет кого-либо из ребят сделать свой собственный бизнес-проект в будущем.
Светлана МИЦКЕВИЧ,
учитель математики категории “учитель-методист” средней школы № 9 Светлогорска,
участница программы “Учитель для Беларуси”




















