Подготовка учащегося к участию в олимпиаде — кропотливая работа. Нужно отметить, что успешно участвовать в предметной олимпиаде может учащийся, знакомый со стандартными приемами решения задач, выходящих за рамки школьного курса.

Определенную роль играет и скорость мышления учащегося. Целесообразно начинать подготовку к предметной олимпиаде с 4—5 классов. Чтобы вовлечь учащегося в олимпиадное движение, необходимо, во-первых, заинтересовать, а во-вторых, создать ситуацию успеха для него. На мой взгляд, логические задачи являются важным инструментом в этом деле.
Почему именно логические? Логические задачи замечательны тем, что легко и непринужденно заставляют думать. Тем самым они повышают мотивацию к изучению предмета. Решать логические задачи очень увлекательно. В них вроде бы нет никакой математики: нет ни чисел, ни формул, ни фигур, но дух математики с ее главной составляющей — математической логикой — присутствует в большей степени. Половина решения любой математической задачи состоит в том, чтобы как следует разобраться в условии, распутать все связи между объектами.
На мой взгляд, наибольшее значение при решении логических задач имеет способность выделять существенное. Поэтому в качестве разминки предлагаю следующее задание.
Имеется ряд слов, в каждом из которых пять даются в скобках, а одно — перед ними. Ваша задача — выбрать два слова, наиболее существенных для слова перед скобками:
Река (берег, рыба, тина, рыболов, вода) — берег, вода.
Пение (звон, голос, искусство, мелодия, аплодисменты) — голос, мелодия.
Чтение (глаза, книга, картина, печать, слово) — глаза, печать.
Игра (шахматы, игроки, штрафы, правила, наказания) — игроки, правила.
В этом задании ответы учащихся могут расходиться. Это свидетельствует о том, что методы их решения отличаются.
После разминки предлагаю задачу, для решения которой необходимо применить метод рассуждений.
В трех банках находятся чай, кофе, сахар. На первой написано “чай”, на второй — “сахар”, а на третьей — “чай или кофе”. Известно, что содержимое ни одной из банок не соответствует надписи на ней.

Рисунок 1. Метод рассуждений
Обращаю внимание учащихся на наиболее существенную фразу. Рассуждения начинаем с объекта с наибольшим количеством информации — третьей банки. В ней находится сахар, соответственно, в двух первых банках находятся чай и кофе. Так как содержимое каждой банки не соответствует надписи на ней, то первая банка наполнена кофе, а во второй находится чай.
Далее считаю важным продолжить метод рассуждения, усложняя задачи. Предлагаю задачу следующего содержания.
Марина, Лариса, Жанна и Катя умеют играть на разных инструментах (пианино, виолончель, гитара, скрипка), но каждая только на одном. Они же знают иностранные языки (английский, французский, немецкий и испанский), но каждая только один.
Известно:
1) Девушка, которая играет на гитаре, говорит по-испански.
2) Лариса не играет ни на скрипке, ни на виолончели и не знает английского языка.
3) Марина не играет ни на скрипке, ни на виолончели и не знает ни немецкого, ни английского.
4) Девушка, которая говорит по-немецки, не играет на виолончели.
5) Жанна знает французский язык, но не играет на скрипке.
На каком инструменте играют и какой иностранный язык знают девушки?
Попробуем решить данную задачу. Сравнивая ее с предыдущими, делаем вывод, что мысленно провести нить рассуждений трудно, так как очень легко запутаться. Для решения таких задач гораздо удобнее свести анализ к системе записей — логических таблиц, где между элементами множеств необходимо установить соответствие. Какие множества у нас имеются? (Имя, язык, инструмент.) Есть ли в условии ключевая фраза, которая поможет вам оттолкнуться? Читаем, делая выводы, и заполняем таблицу с помощью знаков “+” и “–“.
Таблица. Соответствие между элементами множеств
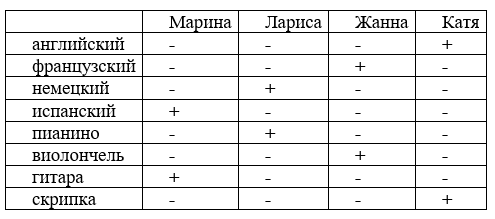
Подобные таблицы широко используются в юридической практике.
Один из наиболее захватывающих видов логических задач — задачи на переливание. А если еще решать их графическим методом, то задачи, подготовленные к занятию, могут закончиться, а учащиеся при этом еще не нарешались.
При решении таких задач необходимо учитывать следующие замечания:
- разрешается наливать в сосуд столько жидкости, сколько в него помещается;
- разрешается переливать всю жидкость из одного сосуда в другой, если она в него вся помещается;
- разрешается отливать из одного сосуда в другой столько жидкости, сколько необходимо, чтобы второй сосуд стал полным.
Каждую задачу на переливание таким методом можно решать двумя способами:
- начать переливания в больший сосуд;
- начать переливания в меньший сосуд.
Если задача имеет решение, то оно получится любым способом, только с разным количеством переливаний.
Рассмотрим пример. Винни Пух запасся 10 литрами меда. У него есть два ведра — 7-литровое и 4-литровое. Как ему разделить мед пополам?
Итак, задача сводится к выделению 5 литров жидкости.
Задачи на переливание жидкостей можно легко решать, двигаясь по бильярдной траектории шара, отражающегося от сторон “ромбической” системы координат.
В рассматриваемой задаче стороны стола должны иметь длины 7 и 4 единицы (объемы меньших сосудов). По горизонтали отложим объем 7-литрового сосуда в любой момент времени, а по вертикали — ту же величину для 4-литрового сосуда.
Изначально шар находится в левой нижней вершине в точке 0. С помощью этого метода можно получить ответ и проследить последовательность, в которой необходимо производить переливания. Наклонные стрелки говорят о том, что вода переливается из одного сосуда в другой, а вертикальные означают, что вода целиком выливается из меньшего сосуда обратно в бесконечный источник либо больший сосуд надо наполнить водой до краев.
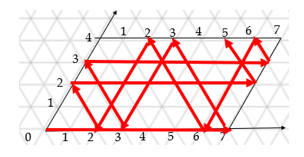
Рисунок 2. Метод бильярдного шара
Использование данного метода даст желаемый результат и при изначальном наполнении сосуда емкости 4.
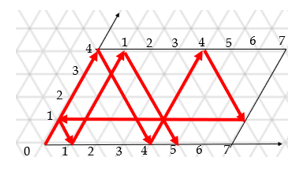
Рисунок 3. Метод бильярдного шара
Что было бы, если в предыдущей задаче емкости были бы объемом 2 и 6 литров?
Если объемы двух меньших сосудов не имеют общего делителя (то есть взаимно просты), а объем третьего сосуда больше или равен сумме объемов двух меньших, то с помощью этих трех сосудов можно отмерить любое целое число литров, начиная с 1 литра и заканчивая объемом среднего сосуда. Такая процедура невозможна, если объемы двух меньших сосудов имеют общий делитель.
Решение логических задач требует повышенного внимания к анализу условия и построению цепочки взаимосвязанных рассуждений, способствует структурированию рассуждений; развивает способность мыслить лаконично, исключать ложное. Решение таких задач — хорошая гимнастика для ума, в результате которой человек становится находчивее и сообразительнее.
Логические задачи практико-ориентированного содержания помогут и в повседневной жизни решать проблемы нестандартным образом.
Татьяна НАЗАРЕНКО,
учитель математики средней школы № 3 Хойников
















